---

---

Citation

Chariots in Space: Preliminary Design Concepts for Low Cost Transportation Systems to Mars by the Use of <i>In-Situ</i> Resources. Sharma, Rahul . Lethbridge Undergraduate Research Journal. Volume 1 Number 2. 2007.

---

Introduction

Cost-effective human exploration of deep space is a tremendously challenging problem. Minimizing flight time and maximize mass delivery are the fundamental requirements for all transportation beyond Low Earth Orbit for all planetary missions, and there is in general an inverse relationship between those two quantities.

Near Earth Asteroids have been nudged by the gravitational attraction of nearby planets into orbits that allow them to enter the Earth's neighborhood. They range in size from small boulders to objects that are hundreds of kilometers in diameter. These pass very close to Earth's orbit around the Sun and evident that hit our planet in past. Concept presented here utilizes the kinetic energy of these objects to transport cargo to Mars while meeting cost, safety and time requirements.

Objectives

This paper outlines the process of utilizing a Near Earth Asteroid to transport cargo to Mars in future for establishing permanent outposts on Mars. This paper has two main focuses.

1. The individual techniques that were utilized for this project in the following areas of selection of candidate asteroids, trajectory, launch, space transport vehicles and operations.
2. The method of optimization that is employed in order to develop a converged design that would meet mission success and time constraints while maximizing safety and minimizing cost.

Approach To The Problem

The whole mission comprises of following sequences of events.

1. Selection of candidate Near Earth Asteroid with specific orbital and physical characteristics.
2. Optimum trajectory analysis of launch opportunities from Earth as well as from lunar base in future.
3. Identification of individual technological requirements specifically for this mission.
4. Cost estimation of the project and comparison with baseline Mars missions.

Solution To The Problem

Candidate Asteroid selection

Asteroids selected for this purpose must be M-class Near Earth Asteroids composed primarily of iron-nickel compound. Their Minimum Orbital Intersection Distance (M.O.I.D) with Earth and Martian orbits must be low. Asteroids must have relatively small eccentricity and inclination as compared to other asteroids. Physical parameters should include high density, low spin and known specific gravity with optimum diameter and additional velocity (ΔV) requirements.

Trajectory

A new trajectory must be found for the mission that intercepts cargo launched from Earth/Lunar launch pads with reasonable ΔV requirements. The ΔV required at each burn and Mars entry velocity needs to be calculated. Additional ΔV is also added in case of difference between inclinations of asteroid and earth orbits.

Technological Requirements

1. An early asteroid warning and detection systems.
2. A highly maneuverable, reusable, cargo transfer vehicle with Mars decent systems.
3. Asteroid rendezvous and operation systems.
4. Advanced scientific payloads for assessment of candidate asteroids.

Cost Estimations

Systems cost is of prime importance to the design. To determine cost, the key assumptions that were made are about specific equipments and hardware design and modifications with design development, testing and integration of hardware. Cost estimation is based on historic data and analyzed previous missions. Launch from a lunar base would be more economically beneficial.

Results

Candidate Asteroid

Selected asteroids for this purpose are within M.O.I.D. limit of 0.02 A.U. for Earth and Mars. All asteroids fulfill the required orbital and physical parameters. Asteroids with diameter ≥ 0.40 km are given here. For the purpose, smaller asteroids can also be used.

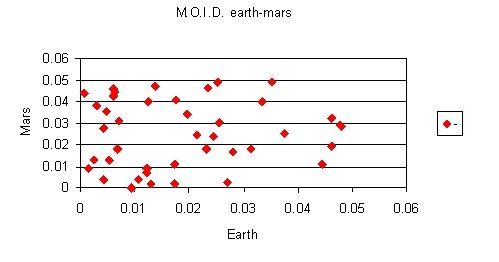
Graph showing comparisons of MOID of asteroids for Earth-Mars orbits.

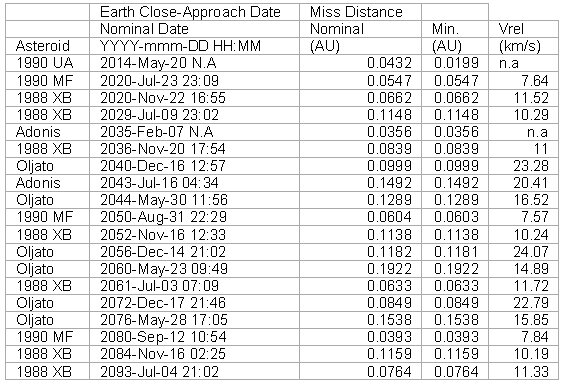
Table 1: Sequence of opportunities.

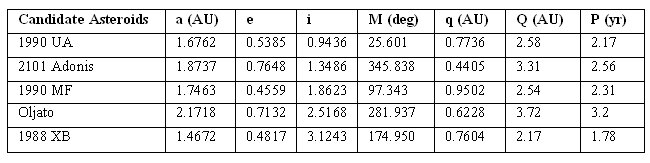
Table 2: Orbital parameters of Candidate asteroids.

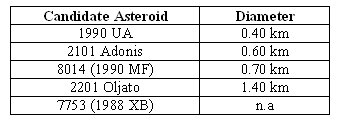
Table 3: Known Physical parameters of candidate asteroids.

Trajectory

Since cost is a prime factor to this concept, hence possibility of assembling and launch from low earth parking orbit and moon launch is also considered.

Launch from parking orbit.

Another possibility for the Earth segment is a launch from a parking orbit, such as a space station. The required change in velocity (ΔV) depends on the radius of the orbit from the center of the Earth.

For example, a launch from a parking orbit at 300 km requires a ΔV of 3.6 km/s, which is much more advantageous than a launch from the surface of Earth.

Launch from lunar base.

Since the lunar sphere of influence is within Earth's sphere of influence, the spacecraft must exit the lunar sphere of influence with the necessary velocity (the lunar hyperbolic excess velocity) to enter a hyperbola that patches to the transfer orbit. This equation determines the lunar hyperbolic velocity.

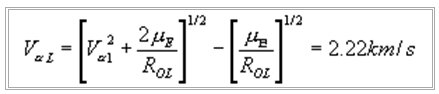
Because the moon rotates only once per month, its rotational velocity is negligible and a launch from anywhere on the moon will require the same ΔV. After determining the lunar hyperbolic excess velocity and the speed necessary to overcome the lunar gravity, the ΔV for a launch from the moon can be calculated to be 3.25 km/s, which is even more advantageous than a launch from a parking orbit.

Therefore, a moon launch requires the smallest ΔV for a cargo transfer to Mars.

The advantages of asteroid transfer can be known by comparing it with other trajectories.

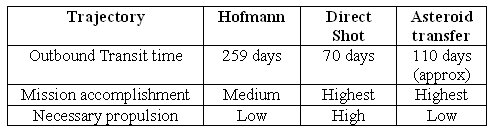
The following are the parameters that can be changed in the trajectory module:

Dates; the absolute departure date and time depending upon the alignment of the planets and energy required to move in between them. This primarily influences the magnitudes of required ΔV.

Wait Time; time that cargo transfer vehicle spends on asteroid before departing for Mars orbit.

Technological Requirements

Detection Systems: Asteroids have very low albedo giving them featureless spectra in the ultraviolet, visible and near infra-red. Hence, the best option which could be utilized for detecting asteroid arrival is by using Doppler radar systems. Radar is not only useful in improving the accuracy of candidate asteroid's orbit, but also a very powerful means of determining physical characteristics such as shape, surface roughness, and rotational rate.

Cargo Transfer Vehicle/Mars Cargo Lander

Baseline vehicle design adopted combines the benefits of hardware availability (i.e. low cost and minimal preparation time), common hardware design, fabrication, and installation procedures, mature technology and reduced operator training. This yields the best low cost, reliability option for this mission.

The Cargo Transfer Vehicle serves both as asteroid lander and in-space transfer vehicle. It consists of two different units which remain as one unit at launch and on asteroid. The aero-braking is used to capture into Mars orbit in the cargo whereas a propulsive burn is used to capture candidate asteroid. The low thrust requirement for lift off from the Moon and LEO enables the same engine to be used for launch, landing, and all in-space propulsive burns.

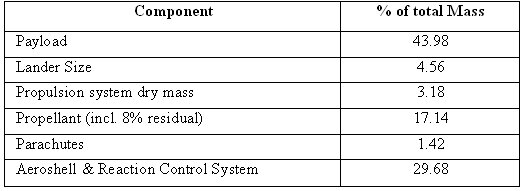
Table 5: CTV Mass Budget

Here, the propellant mass includes total mass required for orbital, trajectory control maneuverings and for retro-burn at Mars orbit. Propellant feed system is scaled from the Space Shuttle Orbital maneuvering system and the parachutes and lander configuration are scaled from NASA's Mars Design Reference Mission version 3.0.

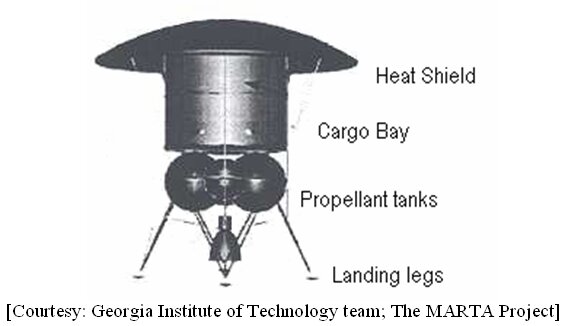
A three-view of the baseline Cargo Transfer Vehicle is shown in figure.

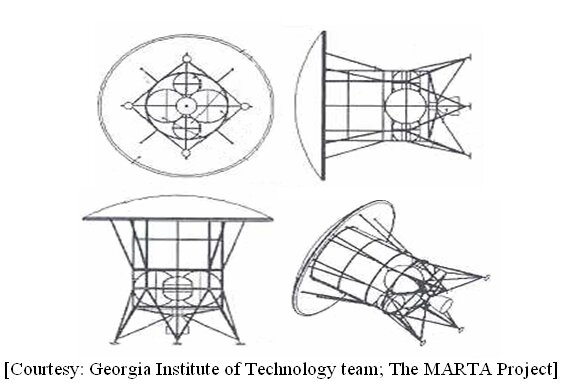
The vehicle is designed to accommodate different configurations. Different payloads can be fitted in the payload compartment either while the Cargo Transfer Vehicle is docked in LEO or on lunar base.

The baseline vehicle is modeled parametrically. The following variables can be changed in the model.

• Scientific payload mass; this provides a mission benefit. Increased payload mass is based on utility with increased cost.
• Propellant mass; this variable is primarily affected by both the required decent and ascent ΔV which drives the required propellant mass.
• Propulsive brake; retro rockets/thrusters and bolstered heat shield part of Mars decent systems by which approach velocity towards Mars can be reduced by aero-braking. It increases mass but also improves safety.
• Landing leg diameter; the diameter of the landing legs when unfold can be modified for increased stability on landing on large candidate asteroid. This increases vehicle weight, cost and safety.

Asteroid Rendezvous Systems

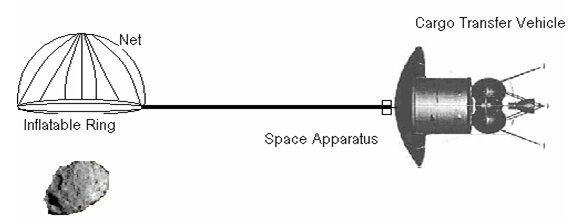
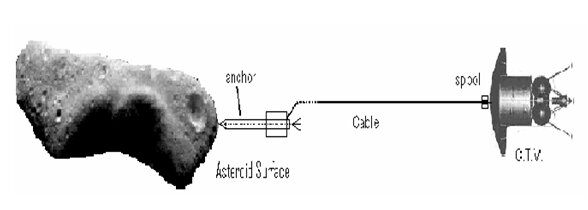
Systems required for our purpose are selected on the basis of physical parameters of the candidate asteroid. From observations, it is known that near earth asteroids vary in shapes; from few to hundred of meters in diameter. To capture small asteroids, net with inflatable ring can be used. While for larger asteroids, anchor with thruster rockets for hammering it into surface of asteroid would require. Both the above configurations are equipped with strong cable, spool, devices for guidance and control of CTV and disconnection systems.

Operations

The Operations discipline encompasses primary areas of manufacturing and integration of cargo vehicle. Components of Cargo Transfer Vehicle (CTV) is launched to low earth orbit (Chapman 1990) or lunar base for assembly. The goal of operations is to place an assembled CTV as quickly as possible at a minimum cost while not compromising safety.

In order to achieve some mentioned goals several key assumptions are made. First, each worker assigned on ground manufacturing and fabrication of cargo transfer vehicle, is assumed to cost current pay scale per year/worker. Second, modification of existing hardware components of vehicle is done parallel, but integration must wait for all components to be modified. The assembly of cargo and vehicle is done in low earth orbit or on lunar base.

The operation module takes, as input the estimated modification and integration times for each of the cargo transfer vehicle sub-systems. The mass of the propellant for orbital and trajectory maneuvering is not launched with CTV hardware. The target launch date is treated as a limit on the time available for departure preparation.

Mission Overview

The mission will begin on Earth with the construction of Cargo Transfer Vehicle and other payload that is required to transport to Mars. These components will be then ferried to an orbiting facility such as International Space Station (ISS) for assembly. During the transit of candidate asteroid, the CTV will descent into orbit using its engines. By thrusters and guidance onboard, CTV would rendezvous with candidate asteroid; depending upon the physical parameters of asteroid.

Case 1: Small asteroid with diameter of few meters

The net is positioned on the trajectory of candidate asteroid, with the net supported in an open position by the inflatable ring and connected to Cargo Transfer Vehicle by cable. The net catches the asteroid and transfers its Kinetic energy to the space vehicle. The space vehicle changes its trajectory, speed and disconnects the cable.

Case 2: Large asteroid with diameter from few hundred meters to larger

The Cargo Transfer Vehicle uses a launcher (a rocket engine) to send anchor to the asteroid. The anchor is connected to the CTV by cable. When the anchor strikes the asteroid surface, a penetrating device makes a deep hole in the asteroid and rocket impulse engines hammers the anchor body into the asteroid. Apparatus on the CTV contains a spool for cable by which CTV can land on the asteroid. The CTV can leave the asteroid surface by giving a signal to the disconnect mechanism.

Mars Descent Scenario: The CTV descent sequence is as follows:

Mars Aero capture: Several minutes before Mars arrival, the CTV separates from candidate asteroid and fires retro rockets to slow down to enter Martian atmosphere at 125 km altitude. The entry flight path must be between 9.8° and 12.4° to capture into orbit around Mars without exceeding the 3.2 g deceleration limit. To capture into a 160 km circular orbit, the CTV would first capture into an elliptical orbit and then airbrake until the apoares fell to 160 km. Then an engine is fired, depending upon the entry parameters, would place it into this low Mars orbit.

Mars Descent: After a final checkout of CTV systems, its reaction control system retrofires to send the lander towards the surface of Mars. At 8 km latitude, work of heat shield is complete, and is jettisoned, the terminal velocity is 650 m/s, and parachute deployment sequence begins. At 1 km latitude, velocity of CTV drops after deployment of supersonic parachutes. The CTV now separates from parachute and ignites the engine on its underside, slowing itself to halt above Martian surface. It may then hover for up to a few seconds before it must touch down on a smooth landing site.

Orbital Transfer Scenario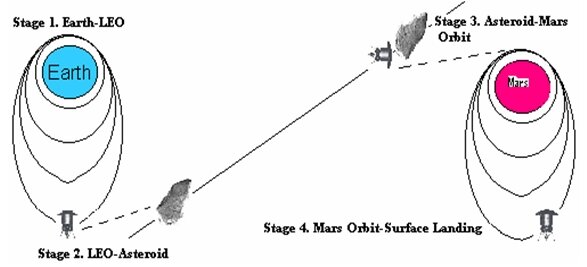

Cost Estimations

Top-level cost estimations were made using Johnson Space Center's web based cost calculators. The cost estimate for development and production was primarily based on mass, and was calculated as dry mass for Cargo Transfer Vehicle as 2 metric tones. In order to have this calculator generate values for each item of operations, it was necessary to be able to calculate component mass from the vehicle dry mass. The extreme cases of the design space were analyzed and items were identified as fixed or variable masses (example; structural mass were a fixed mass for this mission while propellant mass is taken as variable). The variable mass was proportionate to the dry weight remaining after the fixed mass items were removed.

Cost is calculated by breaking the whole mission in sequence and then individual calculations were made for each stage. With an average difficulty level and second level design inheritance, initial operational year is considered as 2012. Difference in total cost is then calculated in percentage savings. The reason for developing the tool in this manner was to allow a single calculator to generate entire cost for the mission and compare it with the baseline missions.

The cost of lunar propellants is treated as independent variable. On available cost of propellants, the reduction in cost of operations was estimated to be approximately 10.04%

Physics Of The Concept

Finding an expression for velocity gained by Cargo Transfer Vehicle (CTV) after connection with the candidate Asteroid.

Here;

m_a = Mass of candidate asteroid u_a = Velocity of asteroid before connecting to CTV v_a = Velocity of asteroid after connecting to CTV m_ctv = Mass of Cargo Transfer Vehicle (CTV) u_ctv = Velocity of CTV before connecting to Asteroid v_ctv = Velocity of CTV after connecting to Asteroid

By the law of conservation of momentum for CTV-Asteroid system;

m_au_a + m_ctvu_ctv = m_av_a + m_ctvv_ctv

Since, for CTV, initial velocity is supposed to be zero, then

m_au_a = m_av_a + m_ctvv_ctv v_a = u_a – m_ctvv_ctv/m_a

Let M = m_ctv/m_a i.e. relative mass of CTV

Therefore, v_a = u_a – Mv_ctv (1)

By the law of conservation of energy

0.5 m_au²_a + 0.5m_ctvu²_ctv = 0.5m_av²_a + 0.5m_ctvv²_ctv

Since u_ctv = 0,

0.5 m_au²_a= 0.5m_av²_a + 0.5m_ctvv²_ctv (2)

Substituting value of v_a from (1) into (2), we get,

m_au²_a = m_a [u_a – Mv_ctv]² + m_ctvv²_ctv m_au²_a = m_au2_a + m_a [M²v²_ctv – 2Mv_ctvu_a] + m_ctvv²_ctv m_a M²v²_ctv + m_ctvv²_ctv = 2Mv_ctv m_au_a m_aM²v_ctv + m_ctvv²_ctv = 2M m_au_a (3)

Dividing equation (3) by m_a, we get

M²v_ctv + m_ctv/m_a v_ctv = 2Mu_a Mv_ctv (M+1) = 2u_aM v_ctv = 2u_a/(M+1) (4) Or v_ctv = 2u_am_a/ (m_ctv + m_a)

Multiply v_ctv both sides in equation (4)

v_ctv² = 2u_av_ctv/ (M+1) v²_ctv (M+1) – 2u_av_ctv + C = 0 (5)

where C is any constant

Let, W is the work done by the spool on CTV to change the length of the cable; then

W = 0.5m_ctvu²_a W = 0.5 M u²_am_a u²_a = 2W/Mm_a

Since, the initial velocity of the asteroid is not changing in this entire process; hence, its square (u² _a) can be taken as constant.

Substituting value of constant in equation (5), we get

(M+1) v²_ctv – 2u_av_ctv + 2W/Mm_a = 0

Let v_ctv = x, then

(M+1) x² – 2u_ax + 2W/Mm_a = 0

Above is a quadratic equation. Solving this for x

x = 2u_a ± [4u² _a – 8W (M+1)/Mm_a]^0.5/2(M+1) Or v_ctv = u_a ± [u²_a – 2W (M+1)/Mm_a]^0.5/ (M+1) (6)

In above expression, if spool on CTV does not change the length of the cable, then W = 0. Also because of asteroid (m_a) is very large as compared to mass of CTV (m_ctv), then can be taken as unity.

Therefore, v_ctv = u_a + [u² _a]^0.5 = 2u_a

i.e. maximum velocity gained by CTV is nearly twice the initial velocity of Asteroid.

If work done by the spool is not zero, then W ≠ 0, the maximum work done by the spool is less than

u²_a – 2W (M+1)/Mm_a ≥ 0 u²_a ≥ 2W (M+1)/Mm_a Mm_au²_a/2(M+1) ≥ W Expression for time taken by CTV to reach the asteroid

For a known (controlled) acceleration “A”;

v²_ctv = 0.5 AT² T = 1/ (0.5A)^0.5 v_ctv T = 1/ (0.5A)^0.5 u_a ± [u²_a – 2W (M+1)/Mm_a]^0.5/ (M+1) Expression for motion of cable from spool on CTV to Asteroid

Let us assume a cable of mass ‘m', length ‘l' and mass per unit length be ‘η'; unwinding from the spool with an angular velocity ‘ω'.

At time, t = 0, the length of the cable be ỷ and at time t, length be y; moving with a speed dy/dt.

In the variable mass problem, equation of motion is m dv/dt = F_ext + V_rel dm/dt (1)

Let v = dy/dt, i.e. change in displacement ‘y' per unit time‘t'. (2)

The mass of entire cable is m = lη (3)

The external force F_ext is the angular force which acts on the length ‘y', the portion of the cable which is unwounded.

Therefore; F_ext = yηω (4)

Using equations (2), (3) and (4) in (1), we get

ln d²y/dt² = yηω + V_rel dm/dt

Assume the system of cable into two parts, one which is unwounded from the spool in space; and the other which is wound on the spool at CTV. As the cable is taut all the times, the speed with which the cable is moving in both the parts must be the same. In other words, the relative speed of the cable is zero. V_rel = 0

Therefore, lη d²y/dt² = yηω

Or, lη d²y/dt² – yηω = 0 (5)

Above is a differential equation,

Equation (5) may be written as

d²y/dt² – y ω/l = 0 (6) d²y/dt² – B²y = 0 (7)

where B² = ω/l

The solution for equation (7) has the form

y = Ae^+Bt + Ce^-Bt (8)

where A and C are constants

At time t = 0, y = ỷ

Therefore, ỷ = A+C

Further, dy/dt = 0, at t = 0.

B (A-C) = 0

A = C

By this, A = C = 0.5 ỷ

Using above expressions in (8), we get

y = 0.5 ỷ [ e^(ω/l)0.5t + e^-(ω/l)0.5t ]

Acceleration of the cable (d²y/dt²) can be given by d²y/dt² = y ω/l {From (6)}

It can be seen that d²y/dt² increases with ‘y', i.e., with the length of the cable unwinding in space. Hence, the motion of the cable is non-uniform acceleration.

Expression for Angular acceleration of the spool on CTV

Let us assume a spool of radius ‘R', and mass ‘M'can rotates freely about a stationary axis. A cable (rope) of mass ‘m', length ‘l', is wounded over the spool with radius ‘r'. The unwounded part in space is ‘y'. Wound part is supposed to have center of mass at spool axis.

Let us use the equation

dM/dt = N; relative to the axis

We should find the angular momentum of the system about the given rotation axis and the corresponding torque N.

The angular momentum is

M = Iω + mvR

Since, moment of inertia (I) = 0.5 MR², and velocity (v) = ωR (assuming no cable slipping)

M = [0.5M + m] R²ω dM/dt = [0.5MR² + mR²] B

where, angular acceleration (B) = dω/dt; change in angular velocity per unit time.

The pulling force on the unwounded part is the only external force, which exerts a torque.

N = (m/l) ya (R-r)

where, ‘a' is the acceleration of the cable in space.

Hence, from the equation

[0.5MR² + mR²] B = (m/l) ya (R-r) B = 2m a y (R-r)/lR² (M+2m) Or, B = 2 m a y (1-r/R)/lR² (M+2m)

Comparison With Other Transportation Technologies

With our understanding of top-level requirements and destination for human exploration, we can assess the characteristics of given concept with other candidate transportation technologies.

Chemical Propulsion

Chemical propulsion (CP) has been used on all previous planetary missions, and so it offers the huge advantage of decades of refinement and flight experience. It provides a relatively high thrust level, which helps to keep flight times low; it can be started and stopped numerous times during a mission; and it has a long lifetime in deep space. However, the maximum specific impulse that can be anticipated for our purposes is only about 350-400 sec. Given this relatively low efficiency, a correspondingly large propellant mass is required in order to deliver the dry mass needed for a human exploration mission within a reasonable flight time. Large propellant load would greatly increase the total mass that must be lifted from the surface of Earth, which is in turn a major driver of launch vehicle size and total mission cost. One option is to use CP only for specific focused tasks, e.g. for Mars orbit insertion or descent burns, for which its high thrust and reliability are of paramount importance.

Electric Propulsion

There are several types of electric propulsion, but for our purposes the class also known as ion propulsion is of greatest interest. Ion propulsion systems use an electrically charged grid to accelerate ions of a propellant (xenon, for example) to very high velocities. Although the thrust produced is very low, when acting over long periods of time in the vacuum of space this technique can provide a large ΔV for a small amount of propellant. While the mass advantages of electric propulsion can be enormous, the downside for human exploration is the low thrust level of these systems. This means that for the destinations of interest to us, flight times may be long compared to chemical propulsion. EP systems do not provide sufficient thrust for rapid departures from LEO or capture into Mars orbit; rather, they must gradually spiral into or out of planetary orbit. They are also not useful for de-orbit prior to descent to the Martian surface, nor for the terminal braking required for soft landing.

Solar Electric

Solar Electric Propulsion (SEP) refers to ion propulsion using electricity derived from solar power. These systems could be an important asset for human exploration, but flight times to Mars would still be relatively long. In addition, solar array degradation due to radiation or micrometeoroid impacts must be considered during the design phase. SEP is likely to be used in a supporting role in overall human exploration architecture.

Nuclear Electric

Nuclear Electric Propulsion (NEP) refers to the use of fission-derived power instead of solar power for electric propulsion. NEP is presently under development within NASA's space science program. NEP can provide a somewhat higher thrust level; it is still by definition a low-thrust system with the flight time disadvantages described earlier. Readiness of the initial flight times cannot be anticipated before 2015.

Thermal Propulsion

From the point of view of mass and flight time, Nuclear Thermal Propulsion (NTP) may well represent the best technology for human exploration beyond the Earth-Moon system. However, although it is well understood in concept, there is no program currently developing NTP flight systems (in contrast to chemical, SEP, and NEP). Thus NTP is a technology for which the entire burden of investment and advocacy would need to be borne by the human exploration program. In addition, there are serious environmental issues and infrastructure investments that would need to be addressed to enable development and testing of NTP technology. Ground tests of NTP rockets would produce effluent gases for which new handling and cleaning facilities would be required. These investments and political concerns are a significant hurdle, and so we assert that the preferred solution is to establish workable first-generation human exploration architecture without relying on NTP.

Solar Sails

Solar sail spacecraft can reach very high velocities and can provide the shortest flight times for certain robotic missions, possibly including interstellar missions. However, for the relatively nearby destinations of interest to us, they carry a significant flight time penalty compared to higher-thrust systems. Even accepting long flight times, transportation of the large masses required for human exploration would imply very large sails, for which deployment and control are serious engineering issues.

Discussions

For cargo transportation concept using asteroids, I had conducted an in-depth investigation of current techniques, for possible LEO/Lunar base launch to Mars, capable of sending large masses of cargo. This investigation was conducted with the goal to reduce transfer cost within the lowest possible time frame while not compromising safety, the architecture was narrowed down to in-situ resources and aero-braking for further investigation.

These technologies were identifies because they reduce the mass of the propellant used and hence cost. Operational costs are the largest expense with propellant costs are the largest contributor. Taking propellant from Earth's surface is an expensive proposition. Hence, In-Situ Resource Utilization (ISRU), the production of materials on Moon surface will be beneficial. However, developing and operating such a system requires further study.

The vehicle was modeled parametrically which incorporates the disciplines of weights and cost. With an up gradation of existing technologies, the overall reduction in terms of cost can be approximately 10.04% of cost now.

Concept presented here provides an advantage of Direct-Shot trajectory at a cost little over the Hofmann transfer trajectory. Many Near Earth Asteroids (NEAs) contain raw material and ore required for manufacturing and production of space systems and colonization. This also provides a unique opportunity to learn about the origin of solar system and primordial history of planets. Asteroid rendezvous missions are a logical step in a spiral approach to human deep space missions. In short, this mission is achievable with current technology, but is only profitable with greater research into enabling technology of ISRU propellant production.

Conclusions

The main conclusion reached from this study is that it is currently possible to build a commercially viable and technologically feasible Earth-Mars cargo transportation system. The Cargo Transfer vehicle presented does not rely on any advanced technologies or any technical advances to become a reality.

However, the most important feature of the architecture is not the vehicle but the knowledge on asteroids is required.

“Human exploration of the Moon is not on the critical path to Mars from the stand point of propulsion technology development, although it may provide a platform for the validation of other mission elements and certainly has some intrinsic science value.”- Douglas Stetson

NEA's offer an opportunity for short duration, low ΔV missions and are a logical step for human activities beyond low earth orbits. Accessible targets provide an opportunity to conduct in situ research, resource as well as test bed for systems necessary for long duration missions in future.

Definition Of Terms

<Π>µ_S = mass of Sun (M_S) times G = 1.32 x 10²⁰ Newton m²/kg ΔV = change of velocity required for a specific maneuver µ_E = mass of Earth (M_E) times G = 3.98 x 10¹⁴ Newton m²/kg R_O = height of orbit plus radius of Earth (R_E) µ_L = mass of Moon (M_L) times G = 4.90 x 10¹² Newton m²/kg R_OL = radius of Moon's orbit = 3.84 x 10⁵ km R_L = radius of Moon = 1738 km V_αL = hyperbolic excess velocity at moon = 11.4 km/s V_αl = hyperbolic excess velocity at Earth = 12.3 km/s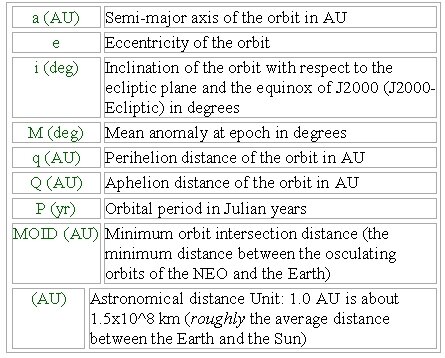

Acknowledgments

I would like to express my utmost gratitude to Dr. P.Venketakrishnan (Senior Professor and Head, Udaipur Solar Observatory) for his guidance and encouragement during every stage of the design. The project could not have taken place without the invaluable experience he helped pass on to me. I would also like to thank the staff at Udaipur Solar Observatory for allowing me to use their library and computer facilities and also faculty at B.N.P.G. College especially Dr. Nira Talesra (Head of Physics Department), for their support and advice throughout the project. Lastly, I would thank Dr. Alexander Bolokin and Dr. Mike Gaffey for their suggested improvements and discussion of the concept.

About the Author

Born on May13, 1984 at Udaipur, India. Youngest of three children to Mr. Nand Kishore Pujari and Mrs. Savitri Sharma, completed school education at Central Academy Senior Secondary School located at Udaipur. Later, joined Bhupal Noble's Post-Graduate College and currently pursuing studies as student of undergraduate Science with major in Physics.

Endnotes

1. "Near Earth Asteroid Program, PHA Orbital Elements"; Available: http://neo.jpl.nasa.gov/elements (August 04, 2005)

2. "MOID for July 2001"; Available: http://www.lowell.edu (August 04, 2005)

3. Kelsey B.Lynn "Which way to Mars? Trajectory Analysis", Available: http://www.stanford.edu/~klynn/mars_paper.html (August 22, 2005)

4. "Free Return Trajectory: Transfer Calculations", Available: http://web.mit.edu/12.000/www/finalpresentation/traj.index9t.html (August 22, 2005)

5. "Minor Planet Center, Close Approaches to the Earth", Available: http://cfa-www.harvard.edu/iau/lists/PHACloseAPP.html (August 29, 2005)

6. Roy A.E., "Orbital Motion", third ed. Pg 383-402, Adam Hilger Publication, Philadelphia, USA 1988

7. NASA Johnson Space Center, Advanced Missions Cost Model; Available: http://jsc.nasa.gov/bu2/AMCM.html (September 04, 2005)

8. Prof. Mike Gaffey, Internet Communication, Oct 2005

9. Dr. Alexander Bolokin, Internet Communication, Nov 2005

10. Vehicle figure adopted from The MARTA Project; Georgia Institute of Technology team, Pg 218, LPI Contribution No. 1063.

11. "Transportation Concepts for Human Space Exploration beyond Low Earth Orbit by Douglas Stetson", Available: http://www.planetary.org/workshop/stetson.html (August 23, 2005).

12. "Step-by-Step Guide to Entry, Descent and Landing", Available: http://marsrovers.jpl.nasa.gov/mission/tl_entry1.html (September 05, 2005)

13. "NASA Human Spaceflight, HSF-The Shuttle", Available: http://spaceflight.nasa.gov/shuttle/reference/oms/gauging, (October, 2005)

14. "Mars Design Reference Mission Version 3.0:, Available: http://ares.jsc.nasa.gov/HumanExplore/Exploration/EXLibrary/docs/MarsRef/addendum/A3.html (October 2005)

15. "Asteroid Earth Approaches", Available: http://www.psi.edu/astdata/earthapp/earthapp.tab (October, 2005).